Κεφάλαια 11 - 18
12. Διαιρέτες ενός αριθμού - ΜΚΔ αριθμών

Πώς βρίσκουμε τον ΜΚΔ δύο ή περισσότερων αριθμών
Θέλω να βρω τον ΜΚΔ των αριθμών 24, 36 και 96.
1ος τρόπος
2ος τρόπος
Θέλω να βρω τον ΜΚΔ των αριθμών 24, 36 και 96.
1ος τρόπος
- Βρίσκω τους διαιρέτες των αριθμών.
- Ξεχωρίζω τους κοινούς διαιρέτες: 1, 2, 3, 4, 6 και 12.
- Ο μεγαλύτερος από τους κοινούς διαιρέτες (ΜΚΔ) είναι ο αριθμός 12.
2ος τρόπος
- Γράφω τους αριθμούς σε οριζόντια διάταξη, κατεβάζω το μικρότερο απ’ αυτούς (24) και τους διαιρώ με αυτόν.
- Κάτω από κάθε αριθμό από τους άλλους γράφω το αντίστοιχο υπόλοιπο από τη διαίρεσή του (δηλαδή 12 κάτω από το 36 και 0 κάτω από το 96).
- Κατεβάζω πάλι το μικρότερο από τους αριθμούς στη 2η σειρά τώρα (12) και διαιρώ τους υπόλοιπους με αυτόν.
- Όταν μείνει μόνο ένας αριθμός και οι υπόλοιποι είναι 0, αυτός είναι ο ΜΚΔ. Έτσι έχουμε ΜΚΔ (24, 36, 96) = 12
13. Κριτήρια διαιρετότητας
15. Παραγοντοποίηση φυσικών αριθμών
Παραγοντοποίηση φυσικών αριθμών
View more presentations or Upload your own.
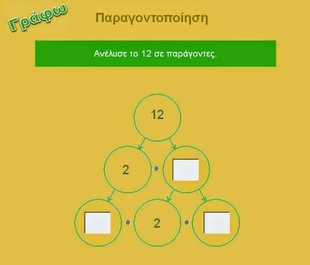
κλικ στην εικόνα

κλικ στην εικόνα
16. Πολλαπλάσια ενός αριθμού - Ε.Κ.Π.
ΠΩΣ ΒΡΙΣΚΟΥΜΕ ΤΟ Ε.Κ.Π.
Α΄ τρόπος
α. Βρίσκουμε μερικά πολλαπλάσια των αριθμών.
β. Σημειώνουμε τα κοινά πολλαπλάσιά τους.
γ. Επιλέγουμε το μικρότερο από αυτά.
Β΄ τρόπος
Παίρνουμε τον μεγαλύτερο αριθμό. Εξετάζουμε αν είναι πολλαπλάσιο ταυτόχρονα των άλλων. Εάν είναι, αυτός είναι και το Ε.Κ.Π. Εάν δεν είναι, παίρνουμε τον διπλάσιό του και εξετάζουμε το ίδιο πράγμα. Εάν δεν είναι και πάλι πολλαπλάσιο των άλλων, παίρνουμε τον τριπλάσιό του και ελέγχουμε ξανά. Συνεχίζουμε με τον ίδιο τρόπο, μέχρι να βρούμε ένα πολλαπλάσιο του μεγαλύτερου αριθμού που να είναι πολλαπλάσιο ταυτόχρονα και των άλλων αριθμών. Αυτό θα είναι και το Ε.Κ.Π.
Παράδειγμα: Θέλουμε να βρούμε το Ε.Κ.Π. των αριθμών 2, 3 και 4.
α. Παίρνουμε το 4. Είναι πολλαπλάσιο του 2, αλλά όχι και του 3.
β. Παίρνουμε το διπλάσιο του 4, το 8. Είναι πολλαπλάσιο του 2, αλλά όχι και του 3.
γ. Παίρνουμε το τριπλάσιο του 4, το 12. Αυτό είναι πολλαπλάσιο και του 2 και του 3.
Άρα: Ε.Κ.Π. (2, 3, 4) = 12.
Γ΄ τρόπος
Παράδειγμα: Θέλουμε να βρούμε το Ε.Κ.Π. των αριθμών 4, 6, 12 και 20.
Ο τρίτος τρόπος, σχηματικά:
Α΄ τρόπος
α. Βρίσκουμε μερικά πολλαπλάσια των αριθμών.
β. Σημειώνουμε τα κοινά πολλαπλάσιά τους.
γ. Επιλέγουμε το μικρότερο από αυτά.
Β΄ τρόπος
Παίρνουμε τον μεγαλύτερο αριθμό. Εξετάζουμε αν είναι πολλαπλάσιο ταυτόχρονα των άλλων. Εάν είναι, αυτός είναι και το Ε.Κ.Π. Εάν δεν είναι, παίρνουμε τον διπλάσιό του και εξετάζουμε το ίδιο πράγμα. Εάν δεν είναι και πάλι πολλαπλάσιο των άλλων, παίρνουμε τον τριπλάσιό του και ελέγχουμε ξανά. Συνεχίζουμε με τον ίδιο τρόπο, μέχρι να βρούμε ένα πολλαπλάσιο του μεγαλύτερου αριθμού που να είναι πολλαπλάσιο ταυτόχρονα και των άλλων αριθμών. Αυτό θα είναι και το Ε.Κ.Π.
Παράδειγμα: Θέλουμε να βρούμε το Ε.Κ.Π. των αριθμών 2, 3 και 4.
α. Παίρνουμε το 4. Είναι πολλαπλάσιο του 2, αλλά όχι και του 3.
β. Παίρνουμε το διπλάσιο του 4, το 8. Είναι πολλαπλάσιο του 2, αλλά όχι και του 3.
γ. Παίρνουμε το τριπλάσιο του 4, το 12. Αυτό είναι πολλαπλάσιο και του 2 και του 3.
Άρα: Ε.Κ.Π. (2, 3, 4) = 12.
Γ΄ τρόπος
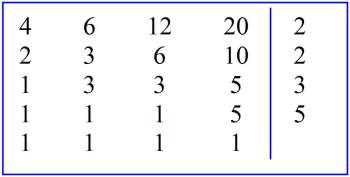
Παράδειγμα: Θέλουμε να βρούμε το Ε.Κ.Π. των αριθμών 4, 6, 12 και 20.
- Γράφουμε τους αριθμούς στην ίδια σειρά. Δεξιά από τον τελευταίο τραβάμε μία κατακόρυφη γραμμή.
- Εξετάζουμε αν ένας τουλάχιστον αριθμός διαιρείται ακριβώς με το 2, και γράφουμε το 2 δεξιά της γραμμής.
(Αν δεν διαιρείται κανείς, πάμε στο 3, αν δεν διαιρείται πάλι κανείς πάμε στο 5, μετά στο 7, στο 11, …)
Στο παράδειγμά μας όλοι διαιρούνται με το 2, έτσι το γράφουμε στα δεξιά και κάτω από το 4, το 6, το 12 και το 20 γράφουμε τα πηλίκα της διαίρεσης κάθε φορά.
- Στην δεύτερη γραμμή που βρήκαμε, υπάρχουν πάλι αριθμοί που διαιρούνται ακριβώς με το 2. Κάνουμε το ίδιο με τα προηγούμενα.
- Στην τρίτη γραμμή δεν υπάρχει αριθμός που να διαιρείται με το 2, αλλά υπάρχουν αριθμοί που διαιρούνται με το 3. Γράφουμε το 3 στα δεξιά και κάνουμε ό,τι και με το 2.
(Όπου υπάρχει το 1, απλώς το ξαναγράφουμε.) - Στην τέταρτη γραμμή δεν υπάρχει αριθμός που να διαιρείται με το 3, υπάρχει όμως αριθμός που διαιρείται ακριβώς με το 5. Γράφουμε το 5 στα δεξιά και κάνουμε ό,τι και προηγουμένως.
- Έτσι καταλήγουμε σε μία νέα γραμμή, όπου όλοι οι αριθμοί είναι μονάδες (το 1), που σημαίναι πως τελειώσαμε τους υπολογισμούς.
- Παίρνουμε τότε τους αριθμούς που βάλαμε δεξιά (το 2, το 2, το 3 και το 5) και τους πολλαπλασιάζουμε. Το γινόμενό τους είναι το Ε.Κ.Π.
Ο τρίτος τρόπος, σχηματικά:
Πηγή: etaksi2011.wordpress.com
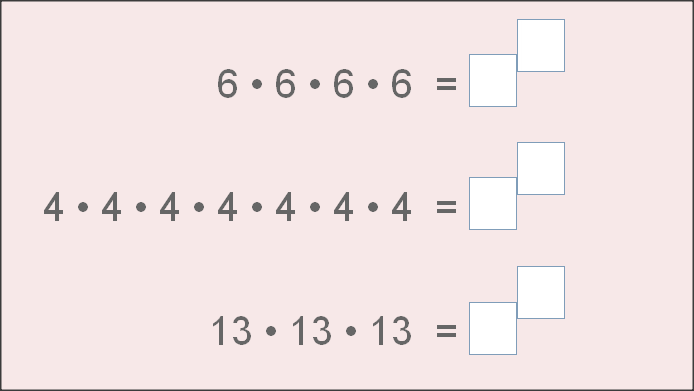
17. Δυνάμεις

κλικ στις εικόνες inschool